Bloque 3
Medidas Estadísticas
Medidas De Tendencia Central
Las características
globales de un conjunto de datos estadísticos pueden resumirse mediante una
serie de cantidades numéricas representativas llamadas parámetros estadísticos.
Entre ellas, las medidas de tendencia central, como la media aritmética, la moda
o la mediana, ayudan a conocer de forma aproximada el comportamiento de una
distribución estadística.
Medidas de centralización
Se llama medidas de
posición, tendencia central o centralización a unos valores numéricos en torno
a los cuales se agrupan, en mayor o menor medida, los valores de una variable
estadística. Estas medidas se conocen también como promedios.
Se distinguen dos
clases principales de valores promedio:
Las medidas de
posición centrales: medias (aritmética, geométrica, cuadrática, ponderada),
mediana y moda.
Media
La media, también conocida como promedio, es
el valor que se obtiene al dividir la suma de un conglomerado de números entre
la cantidad de ellos.
Algunas
características de la media son:
Considera todas las
puntuaciones
El numerador de la
fórmula es la cantidad de valores
Cuando hay
puntuaciones extremas, no tiene una representación exacta de la muestra
Mediana
La media aritmética no
siempre es representativa de una serie estadística. Para complementarla, se
utiliza un valor numérico conocido como mediana o valor central.
Dado un conjunto de
valores ordenados, su mediana se define como un valor numérico tal que se
encuentra en el centro de la serie, con igual número de valores superiores a él
que inferiores. Normalmente, la mediana se expresa como Me.
La mediana es única
para cada grupo de valores. Cuando el número de valores ordenados (de mayor a
menor, o de menor a mayor) de la serie es impar, la mediana corresponderá al
valor que ocupe la posición (n + 1) /2 de la serie. Si el número de valores es
par, ninguno de ellos ocupará la posición central. Entonces, se tomará como
mediana la media aritmética entre los dos valores centrales.
Moda
La moda es el valor
que aparece más dentro de un conglomerado. En un grupo puede haber dos modas y
se conoce como bimodal, y más de dos modas o multimodal cuando se repiten más
de dos valores; se llama amodal cuando en un conglomerado no se repiten los
valores.
Por último, se conoce
como moda adyacente cuando dos valores continuos tienen la misma cantidad de
repeticiones. En este caso se saca el promedio de ambos.
Las principales
características de la moda son:
Es una muestra muy
clara
Las operaciones para
determinar el resultado son muy fáciles de elaborar
Los valores que se
presentan pueden ser cualitativos y cuantitativos
Sesgo
En estadística se
llama sesgo de un estimador a la diferencia entre su esperanza matemática y el
valor numérico del parámetro que estima. Un estimador cuyo sesgo es nulo se
llama insesgado o centrado.
El no tener sesgo es
una propiedad deseable de los estimadores. Una propiedad relacionada con esta
es la de la consistencia: un estimador puede tener un sesgo, pero el tamaño de
este converge a cero conforme crece el tamaño muestral.
Dada la importancia de
la falta de sesgo, en ocasiones, en lugar de estimadores naturales se utilizan
otros corregidos para eliminar el sesgo. Así ocurre, por ejemplo, con la
varianza muestral.
Medidas de Dispersión
Las medidas de
dispersión, variabilidad o variación nos indican si esos datos están próximos
entre sí o sí están dispersos, es decir, nos indican cuán esparcidos se
encuentran los datos. Estas medidas de dispersión nos permiten apreciar la
distancia que existe entre los datos a un cierto valor central e identificar la
concentración de los mismos en un cierto sector de la distribución, es decir,
permiten estimar cuán dispersas están dos o más distribuciones de datos.
Estas medidas permiten
evaluar la confiabilidad del valor del dato central de un conjunto de datos,
siendo la media aritmética el dato central más utilizado. Cuando existe una
dispersión pequeña se dice que los datos están dispersos o acumulados
cercanamente respecto a un valor central, en este caso el dato central es un
valor muy representativo. En el caso que la dispersión sea grande el valor
central no es muy confiable. Cuando una distribución de datos tiene poca
dispersión toma el nombre de distribución homogénea y si su dispersión es alta
se llama heterogénea.
Desviación media o desviación promedio
La desviación media o
desviación promedio es la media aritmética de los valores absolutos de las
desviaciones respecto a la media aritmética.
PROPIEDADES
Guarda las mismas dimensiones
que las observaciones. La suma de valores absolutos es relativamente sencilla
de calcular, pero esta simplicidad tiene un inconveniente: Desde el punto de
vista geométrico, la distancia que induce la desviación media en el espacio de
observaciones no es la natural (no permite definir ángulos entre dos conjuntos
de observaciones). Esto hace que sea muy engorroso trabajar con ella a la hora
de hacer inferencia a la población.
MÉTODOS DE CÁLCULO
1.-Para Datos No Agrupados
2.-Para Datos
Agrupados en Tablas de Frecuencia
Rango
El rango es un valor
numérico que indica la diferencia entre el valor máximo y el mínimo de una
población o muestra estadística. El rango suele ser utilizado para obtener la
dispersión total. El rango es muy útil
para observar cuán grande podría llegar a ser una variación o cambio. Vale la
pena mencionar también que, en no pocas ocasiones, el rango no es una medida
fija.
Fórmula del rango
Para calcular el rango
de una muestra o población estadística utilizaremos la siguiente fórmula:
R = Máx. x – Mín. x
Donde
R es el rango.
Máx. es el valor
máximo de la muestra o población.
Mín. es el valor
mínimo de la muestra o población estadística.
x es la variable sobre
la que se pretende calcular esta medida.
Para ello, no es
necesario ordenar los valores de mayor a menor o viceversa. Si sabemos cuál son
los números con mayor y menor valor, tan sólo tendremos que aplicar la fórmula.
Varianza
La varianza de una
muestra o de un conjunto de valores, es la sumatoria de las desviaciones al
cuadrado con respecto al promedio o a la media, todo esto dividido entre el
número total de observaciones menos 1.
De manera muy general
se puede decir que la varianza es la desviación estándar elevada al cuadrado.
La varianza de una
muestra se simboliza como S2, mientras que la varianza de una población de
simboliza como σ2.
La varianza de una
muestra es utilizada para estimar la varianza de una población, la cual en
muchas ocasiones se desconoce. Es por esto que S2 también es considerada
comúnmente como un estadístico y σ2 como un parámetro.
Fórmula de la Varianza
La varianza de una
muestra presenta la siguiente fórmula:
Donde, representa la
sumatoria de la resta entre cada uno de los valores muestreados () y la media
(), elevado al cuadrado.
A su vez, representa
el número total de observaciones o datos muestreados. Para valores muy grandes de
la varianza es mínima o incluso despreciable.
En cambio, la varianza
de una población presenta la siguiente fórmula:
Donde N representa el
número total de observaciones o datos muestreados.
En la mayoría de los
casos es muy difícil, por no decir imposible obtener un N total de datos, por
ejemplo, al hablar de individuos de una población, no es posible muestrear a
todos estos individuos, ya que existe un factor de tiempo y recursos limitante.
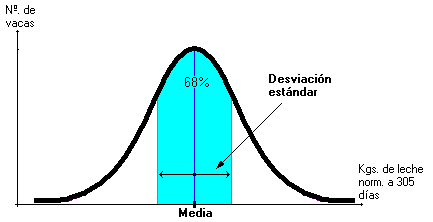
Desviación Estándar
La desviación estándar
es la medida de dispersión más común, que indica qué tan dispersos están los
datos con respecto a la media. Mientras mayor sea la desviación estándar, mayor
será la dispersión de los datos.
El símbolo σ (sigma)
se utiliza frecuentemente para representar la desviación estándar de una
población, mientras que s se utiliza para representar la desviación estándar de
una muestra. La variación que es aleatoria o natural de un proceso se conoce
comúnmente como ruido.
La desviación estándar
se puede utilizar para establecer un valor de referencia para estimar la
variación general de un proceso.
Cuartiales
Los cuartiles son
valores que dividen una muestra de datos en cuatro partes iguales. Utilizando
cuartiles puede evaluar rápidamente la dispersión y la tendencia central de un
conjunto de datos, que son los pasos iniciales importantes para comprender sus
datos. Los cuartiles son los tres valores de la variable que dividen a un
conjunto de datos ordenados en cuatro partes iguales.
Q1, Q2 y Q3 determinan
los valores correspondientes al 25%, al 50% y al 75% de los datos. Q2 coincide
con la mediana.
Deciles
Los deciles son los
nueve valores que dividen la serie de datos en diez partes iguales. Los deciles
dan los valores correspondientes al 10%, al 20%... y al 90% de los datos.
D5 coincide con la
mediana.
Cálculo de los deciles
Percentiles
Los percentiles son
los 99 valores que dividen la serie de datos en 100 partes iguales. Los
percentiles dan los valores correspondientes al 1%, al 2%... y al 99% de los
datos.
P50 coincide con la
mediana.
Cálculo de los
percentiles
En primer lugar,
buscamos la clase donde se encuentra.
En la tabla de las frecuencias acumuladas.
En la tabla de las frecuencias acumuladas.


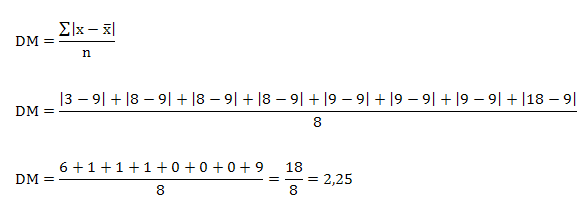


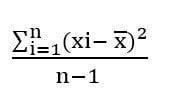
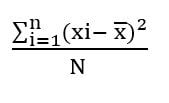






Comentarios
Publicar un comentario